在现实生活中,我们经常需要从一堆样本中找出相似度较高的样本对。比如考试作弊查重,就是需要从一堆答卷中找出重复文本较多的答卷对。在定义了样本对的相似度计算方法后,我们可以枚举所有的样本对,计算其相似度,检验其值是否超过预先给定的相似度阈值,据此判断该样本对是否是相似度较高的样本对。假设总共有 $n$ 个样本,那么这种做法就需要计算 $O(n^2)$ 个样本对的相似度。但在实际应用中,相似度较高的样本对往往是较少的,数量远少于 $O(n^2)$ 这个数量级。因此,我们希望能有一种算法,以较小的时间复杂度找到少量的需要计算相似度的样本对(换句话说,原先是将全体样本对当成相似样本对候选,现在我们希望能减少相似样本对候选的数量),局部敏感哈希(Locality-Sensitive Hashing)就是这样的方法。本文将以寻找相似文本文档对为例,来介绍局部敏感哈希的使用方法。
本文考虑的任务是从 $n$ 个文本文档中寻找较相似的文本文档对。此处的相似,指的是文本意义上的相似,即对于两个文本文档,重复的片段越多,我们就认为它们越相似。在考虑文本文档的文本意义上的相似性时,人们常常先将文本文档转化为连续字符串的集合(这个过程称为shingling),再将集合对的Jaccard相似度(Jaccard Similarity)作为文本文档对的相似度。本节将依次介绍shingling和Jaccard相似度。
文本文档的Shingling(shingle大概指的是连续字符串,shingling大概就是“shingle化”的意思,即把文本文档变成shingle的集合)就是将文本文档转化为文本文档中全体长度为 $k$ 的连续字符(或单词)串的集合,其中 $k$ 是一个预先给定的正整数。举个例子,假设 $k=2$,文本文档的内容是“锟斤拷烫烫烫”,那么将该文档shingling后得到的集合是:{锟斤,斤拷,拷烫,烫烫},我们将这个集合称为文本文档的集合表示。文本文档的shingling总结如下。
Jaccard相似度是描述两个集合相似程度的相似性度量函数,对于两个集合,它们交集的元素个数和并集的元素个数之比就定义为Jaccard相似度。Jaccard相似度总结如下。
对于两个文本文档,如果它们的重复片段很多,那么它们的长度为 $k$ 的字符串的重复率也会很高,从而它们的集合表示也很相似。因此在文本文档的集合表示上算Jaccard相似度能较好反映文本文档在文本意义上的相似程度。
在介绍局部敏感哈希之前,我们先回顾一下本文需要解决的任务,将其总结如下。
很容易给出一个暴力算法:计算全体文本文档对的相似度,检验其是否不小于 $s$,将其总结如下。
- 遍历全体文本文档对,计算相似度,检验是否不小于 $s$,若是,则为相似文本文档对。
但这个暴力算法将全体文本文档对都作为相似文本文档对候选,逐一计算相似度,也就是要计算 $O(n^2)$ 个文本文档对的相似度。但实际上真正的相似文本文档对的数目可能远远少于 $O(n^2)$ 这个量级。比如在我们考虑的任务中,大部分文本文档可能都是原创的,也就是大部分文本文档对之间没有太多相同的片段,从而在文本意义上不会太相似。因此我们希望能有一种算法,以尽量小的时间复杂度,筛选出尽量少的相似文本文档对候选,而不是简单地将全体文本文档对都当作候选。局部敏感哈希这个技术就能实现这样的功能,这个技术的想法是这样的:针对具体任务,设计合适的哈希函数,将全体文本文档映射到若干个桶中。并且这个哈希函数要保证相似的文本文档对能以较大的概率映射到同一个桶,不相似的文本文档对能以较大的概率映射到不同的桶。有了这样的哈希函数,我们就能以 $O(n)$ 的时间复杂度将全体文本文档分到不同桶里,并且只需将同一个桶中的文本文档对作为相似文本文档对候选即可,这样就减少了相似文本文档对候选的数量。
我们先介绍一个名为最小哈希(Min Hash)的哈希函数族,这是一族带参数的哈希函数,参数是 $1,2,\dots,M$ 的排列。在给定一个 $1,2,...,M$ 的排列后,对应的最小哈希函数能将一个 $M$ 维的0-1向量映射到 $\{1,2,...,M\}$ 中的一个数。在介绍最小哈希之前,我们需要先把文本文档的集合表示转化为0-1向量表示。假设全体文本文档的集合表示中总共有 $M$ 个不同的字符串,依次编号为 $1,2,\dots,M$。那么对每个文本文档,它的0-1向量表示是一个 $M$ 维的0-1向量,如果编号为 $i$ 的字符串出现在它的集合表示中,那么它的0-1向量表示的第 $i$ 维就是 $1$,否则就是 $0$。举个例子,假设我们总共有 $3$ 个文本文档,并且它们的集合表示如下所示。
- $S_1=\{ab,bb,bc,cd\}$
- $S_2=\{bb,bc,cd,eb\}$
- $S_3=\{ad,ca,de,eb\}$
那么,连续字符串的全集是 $S=\{ab,ad,bb,bc,ca,cd,de,eb\}$,将它们依次编号为 $1,2,\dots,8$。则这 $3$ 个文本文档的0-1向量表示如下所示。
- $V_1=(1,0,1,1,0,1,0,0)$
- $V_2=(0,0,1,1,0,1,0,1)$
- $V_3=(0,1,0,0,1,0,1,1)$
有了文本文档的0-1向量表示,我们就可以回过头来继续介绍最小哈希。最小哈希函数是带参数的哈希函数,这个参数是 $1,2,\dots,M$ 的一个随机排列。假设这个排列的值是 $(a_1,a_2,\dots,a_M)$,那么输入一个 $M$ 维的0-1向量表示后,依次遍历它的第 $a_1$ 维,第 $a_2$ 维,$\dots$,第 $a_M$ 维,将遍历过程中第一个值为 $1$ 的维度作为哈希函数的输出。仍然以上面的 $3$ 个文档为例,假设最小哈希的参数为 $(4,3,5,6,1,7,2,8)$,那么对于第一个文本文档,它的0-1向量表示的第 $4$ 维的值就是是 $1$,所以它的哈希值是 $4$,同理,第二个文本文档的哈希值也是 $4$,对于第三个文本文档,它的0-1向量表示的第 $4$ 维和第 $3$ 维都是 $0$,第 $5$ 维才是 $1$,因此它的哈希值是 $5$。最小哈希总结如下。
最小哈希有个特殊的性质,就是两个文本文档,它们的0-1向量表示的signature相等的概率恰好等于它们的相似度(换句话说,它们被随机选取的最小哈希函数映射到同一个桶的概率恰好等于它们的相似度),这个性质用数学语言表述如下所示。
我们来简单地证明一下这个性质:考虑排列 $A$ 中第一个满足 $V_{1,i}=1$ 或 $V_{2,i}=1$ 的下标 $i$,这样的下标总共有 $|S_1\cup S_2|$ 种可能。而 $h_A(V_1)=h_A(V_2)$ 当且仅当 $V_{1,i}=1$ 并且 $V_{2,i}=1$,这样的下标总共有 $|S_1\cap S_2|$ 种可能。因此 $$P\{h_A(V_1)=h_A(V_2)\}=\frac{|S_1\cap S_2|}{|S_1\cup S_2|}=Jaccard(S_1,S_2)$$
根据这条性质,我们可以画出 $P\{h_A(V_1)=h_A(V_2)\}$ 和 $Jaccard(S_1,S_2)$ 的函数关系曲线,如下所示,其中横轴代表 $Jaccard(S_1,S_2)$,纵轴代表 $P\{h_A(V_1)=h_A(V_2)\}$,$s_0$ 是给定的相似度阈值。
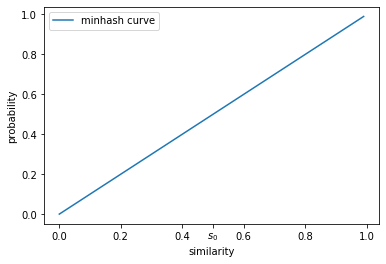
从上图中我们可以看到,随着两个文本文档相似度的增大,最小哈希将它们映射到同一个桶的概率是在逐渐增大的。但即使两个文本文档的相似度大于 $s_0$,最小哈希仍然以较大的概率不将它们映射到同一个桶,这将造成大量的false negative。另一方面,即使两个文本文档的相似度小于 $s_0$,最小哈希仍然以较大的概率将它们映射到同一个桶,这将大大增加相似文本文档对候选的数量,导致最终仍然需要计算相当多数量的文本文档对的相似度。因此上图的曲线并不理想,理想状态下的曲线应该如下图所示的那样,当文本文档对的相似度小于 $s_0$ 时,以接近 $0$ 的概率将它们映射到同一个桶,当文本文档对的相似度大于 $s_0$ 时,以接近 $1$ 的概率将它们映射到同一个桶。
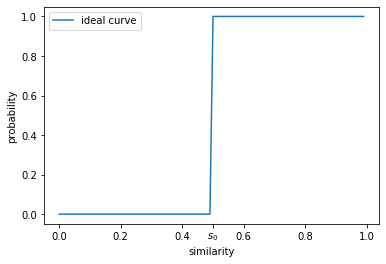
我们称上图这样的曲线为“局部敏感”的曲线,因为它只在 $s_0$ 的局部变化地比较剧烈。局部敏感哈希就是将一个不太“局部敏感”的哈希函数族改造成“局部敏感”的哈希函数族的一种技术。
这里给出对最小哈希函数族进行改造的一个例子。首先我们从最小哈希函数族中随机选取 $m=b\times r$ 个最小哈希函数,将其分为 $b$ 组,每组有 $r$ 个最小哈希函数。每一组的 $r$ 个最小哈希函数将全体文本文档映射到 $r$ 维的signature,两个文本文档被这组哈希函数映射到同一个桶里,当且仅当 $r$ 个signature都完全相同(这相当于把原先的 $1$ 维的桶换成了 $r$ 维的桶,桶的数量从 $M$ 增加到了 $M^r$,这使得同一个桶中文本文档的数量大大减少)。然后由于我们总共有 $b$ 个组的最小哈希函数,因此我们有 $b$ 组桶(这相当于把每个文本文档都映射到 $b$ 个桶中,增大了相似文本文档出现在同一个桶中的概率),需要注意每一组的桶都是不一样的(相当于总共有 $b\times M^r$ 个桶,但大部分桶可能都是空的)。最后我们将全体桶中的文本文档对都作为相似文本文档对候选。将上述改造过程总结如下所示(注意这里并没有给出改造后的哈希函数族的具体函数表达式,只是给出“哈希值相等”的定义)。
- 设 $\{h_A\}$ 是一族以 $A$ 为参数的哈希函数族,将哈希函数的输入简称为输入。
- 均匀随机地从 $\{h_A\}$ 中选取 $m=b\times r$ 个哈希函数,将其分为 $b$ 组,每组 $r$ 个哈希函数,得到 $\{h_{A_{bb,rr}}\}_{bb=1,2,\dots,b;rr=1,2,\dots,r}$
- 对每个输入,计算 $m$ 个哈希函数值。认为输入 $x$ 和输入 $y$的哈希值相同,当且仅当存在 $bb\in\{1,2,\dots,b\}$,使得 $$h_{A_{bb,rr}}(x)=h_{A_{bb,rr}}(y),\forall rr\in \{1,2,\dots,r\}$$
- 注:这里是先进行“与”操作,再进行“或”操作来改造函数族的,实际上也可以用其它的“与”“或”操作序列进行改造。
对最小哈希函数族进行上述改造后,我们仍然可以计算两个相似度为 $s$ 的文本文档出现在同一个桶的概率。对每个最小哈希函数组,这两个文本文档出现在同一个 $r$ 维桶的概率是 $s^r$,因此不出现在同一个 $r$ 维桶的概率就是 $1-s^r$。总共有 $b$ 组最小哈希函数组,两个文档全部都不出现在同一个 $r$ 维桶的概率是 ${(1-s^r)}^b$(有 $b$ 组不同的 $r$ 维桶),因此这两个文本文档出现在至少一组 $r$ 维桶的同一个 $r$ 维桶的概率是 $1-{(1-s^r)}^b$。当 $m=100,b=20,r=5$ 时,相似度为 $s$ 的文本文档对成为相似文本文档对候选的概率是 $1-{(1-s^5)}^{20}$,函数曲线如下图所示。可以看到,虽然这个曲线没有理想状态下的曲线那么完美,但相比于最小哈希的曲线有了巨大的进步。
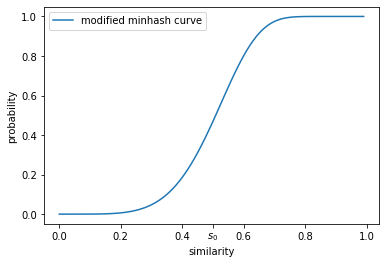
至此,我们就成功在 $O(n)$ 的时间复杂度内将全体文本文档分到各个桶里面,并只需将同一个桶里的文本文档对当成相似文本文档对候选。只要真正的相似文本文档对数量不多,那么这个方法得到的相似文本文档对候选的数量也会不多。由于这个算法是一个随机算法,因此会有相似度达到阈值的文本文档对没有被映射到同一个桶的情况(即false negative),但我们可以通过调参(比如增大$b$,减小$r$)来增加相似文本文档对候选的数量,从而减少false negative的数量。
最后让我们来总结一下本文的内容。本文主要以寻找相似文本文档对为例,介绍了局部敏感哈希的使用方法。下图是整个算法的流程图。
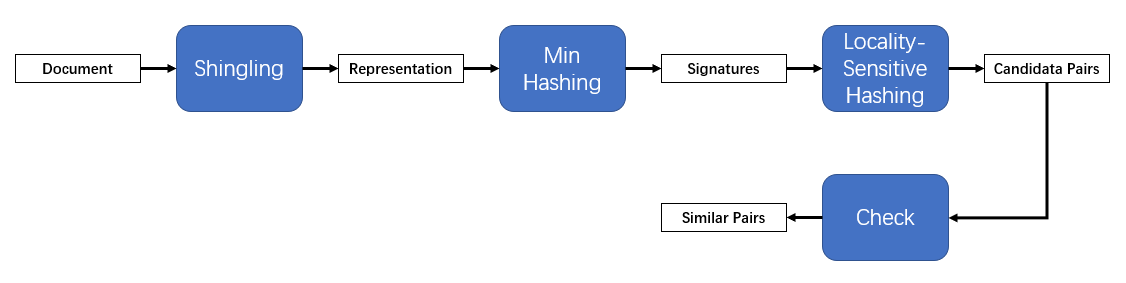
我们来根据这个图总结一下算法的流程。首先,我们先将文本文档shingling,得到文本文档的集合表示,再整合全体集合表示,用 $M$ 维的0-1向量表示来表示文本文档。然后我们从最小哈希函数族中均匀随机地选取了 $m$ 个最小哈希函数来对每个文本文档计算 $m$ 个signature值。根据这些signature值,使用局部敏感哈希定义的规则来得到相似文本文档对候选。最后计算每一对相似文本文档对候选的相似度,检验其是否是真正的相似文本文档对。这就是整个算法的流程,相比于暴力算法,局部敏感哈希大大减少了相似文本文档对候选的数量,减少了算法的时间开销。
[1]CS246 of Stanford University, Week 3
[2]Mining of Massive Datasets, Chapter 3